Les polygones réguliers
Le carré et l'octogone inscrit
l'hexagone et le triangle
équilatéral inscrits
Surface des polygones réguliers
Définitions.
Les polygones réguliers sont des polygones qui ont tous leurs côtés égaux et leurs angles égaux.
Les points où les côtés se rencontrent sont les sommets du polygone.
Un polygone est dit inscrit dans un cercle, lorsqu'il a tous ses sommets sur la
circonférence.
Le carré et l'octogone inscrit.
Menons dans un cercle deux diamètres perpendiculaires. Joignons les extrémités: Nous avons un carré inscrit.
Menons ensuite deux diamètres perpendiculaires aux côtés du carré : Nous pouvons tracer un octogone régulier.
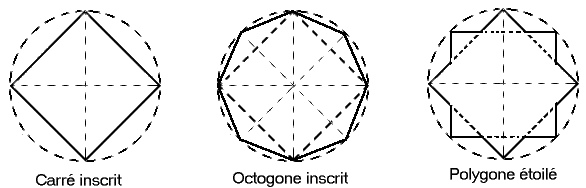
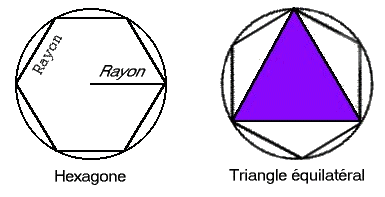
L'hexagone et le triangle équilatéral inscrits.
Portons bout à bout des cordes égales au rayon : nous avons divisé la
circonférence en sis arcs égaux. En loignant les
points de division, nous avons un hexagone régulier.
Le triangle équilatéral est obtenu en joignant deux à deux les sommets
de l'hexagone.
Surface des polygones réguliers.
En joignant les sommets du polygone au centre, on obtient autant de
triangles isocèles qu'il y a de côtés.
La hauteur, égale dans tous ces triangles, est appelée l'apothème.
La surface de l'un des triangles est égale au demi-produit du côté par l'apothème
:

Surface du triangle = côté x apothème : 2
Par conséquent, on a pour la surface du polygone régulier de n côtés
:
Surface du polygones = n fois surface du triangle
= n côtés x apothème : 2
Surface du polygone = périmètre x apothème : 2
|
La surface d'un
polygone régulier est égale au demi produit du périmètre par l'apothème. |
Rev 01.0928.006